How Revs squeezes complex track layouts into extremely small data files
The original 1985 release of Revs comes bundled with just one track: the iconic Silverstone. The data for this track is separated out into its own data file, rather than being integrated into the main game binary, with the idea being that Acornsoft could release more tracks by simply providing additional data files in the same format as Silverstone, thereby extending the scope and appeal of the original game. This was pretty forward-thinking stuff from author Geoff Crammond, and it worked well, with the Revs 4 Tracks expansion arriving in time for Christmas later that year.
But there's a problem with this approach, as the track data file format used for Silverstone, which is described in the deep dive on the track data file format, turns out to have a serious limitation. To see what it is, take a look at this map of the Silverstone track, as extracted from the game data:
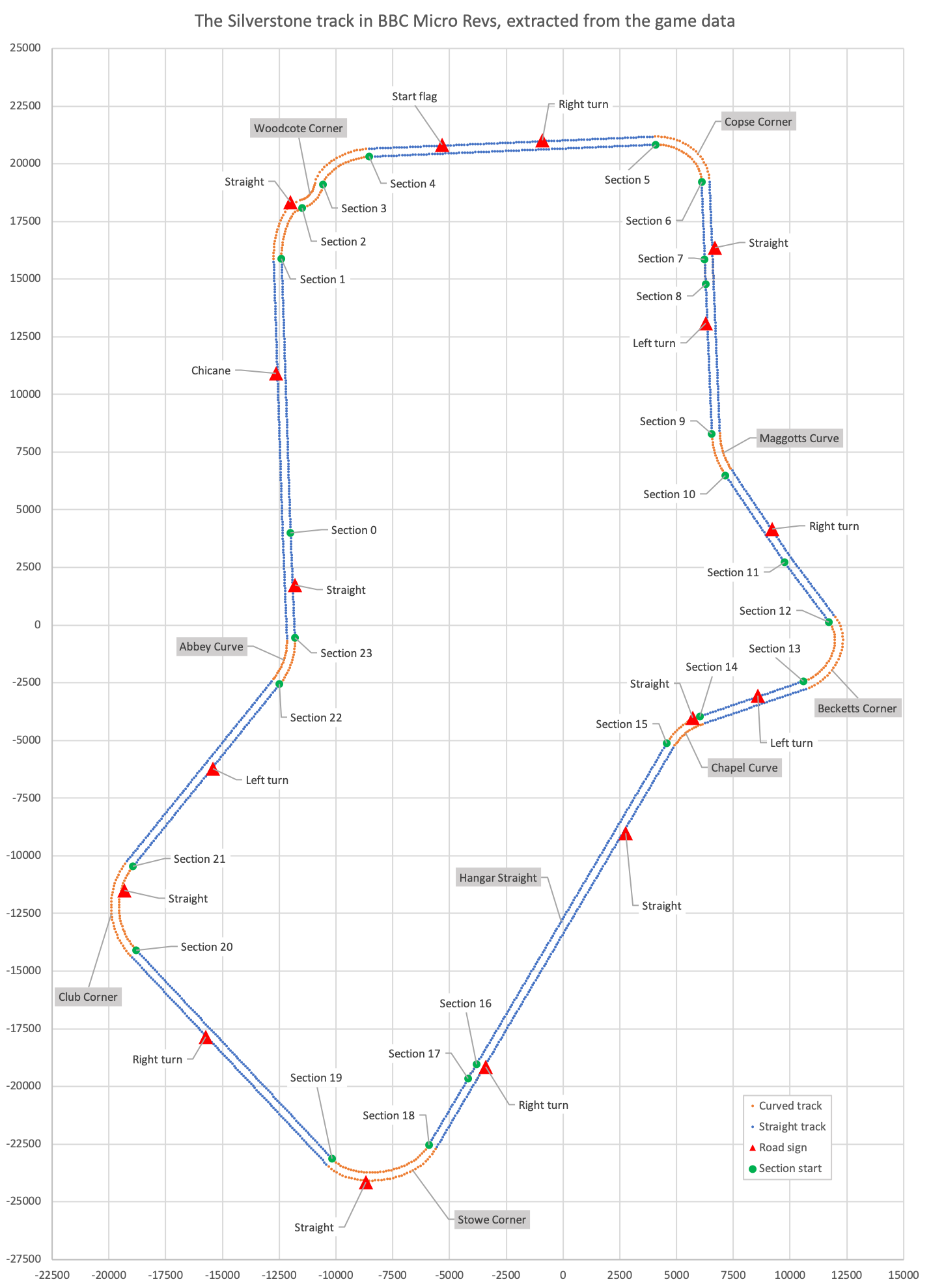


Straight sections are shown in blue, while curved sections are in orange, and you can see that Silverstone is mainly made up of straight sections, with a handful of short curved sections between. But now take a look at Oulton Park, one of the tracks that comes with the Revs 4 Tracks expansion. This is what the track looks like when extracted from the game data:
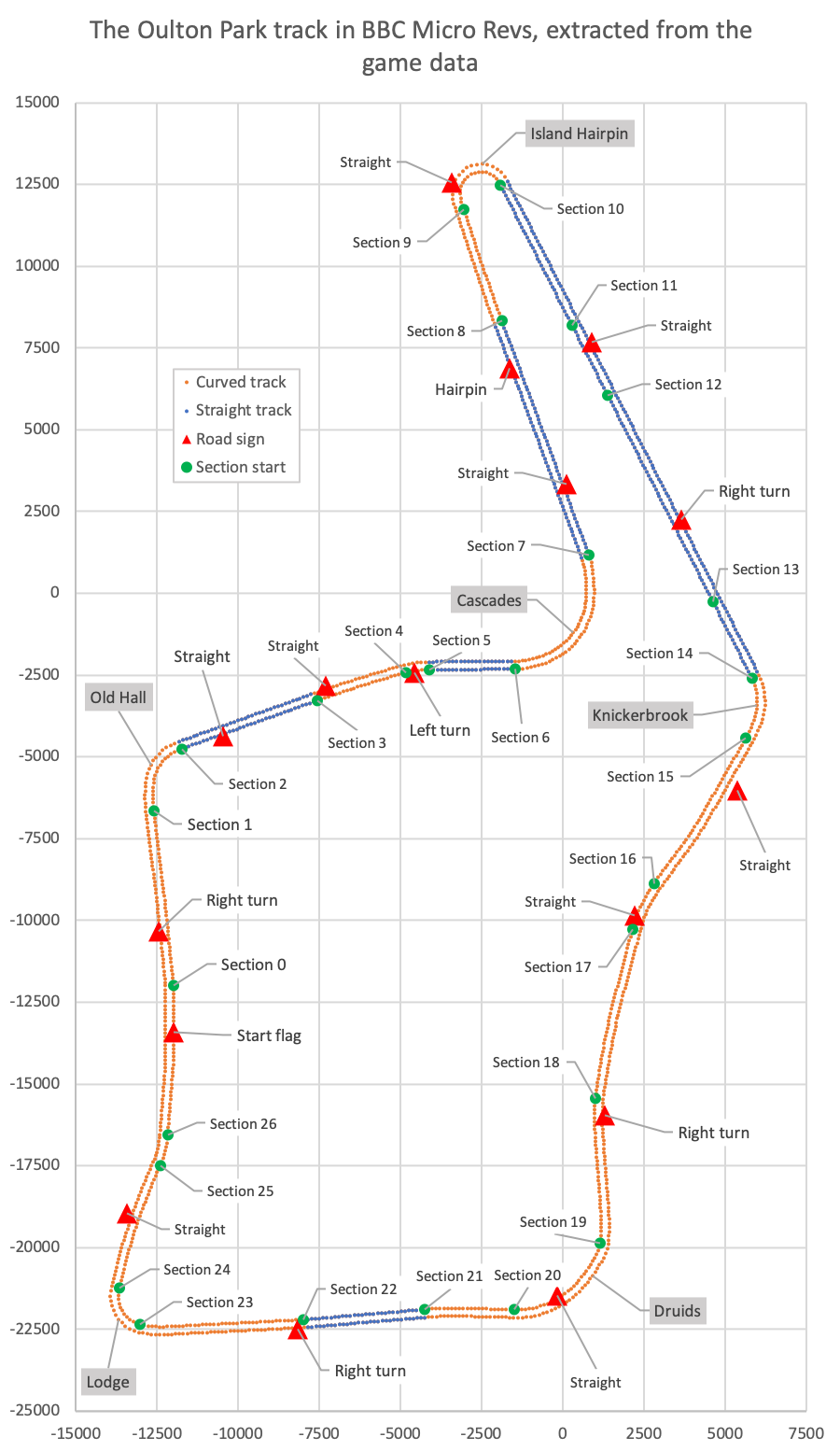

This is a really curvy track when compared to Silverstone, and the balance of orange to blue is the other way around. Unfortunately, this turns out to be a problem. The track data file format stores straight sections efficiently; a straight can be described using just one vector, namely the vector from one segment to the next as we work our way along the straight, stepping from one blue dot to the next. This vector is the same for every step along the straight line, but for curved sections, the vector is different for each step along the track, i.e. when stepping from one orange dot to the next. This makes curves much more memory-hungry, as we need to store lots of segment vectors rather than just one.
So because Silverstone is essentially a set of straights, connected by relatively small corners, it fits nicely into the track file, but because Oulton Park is full of curves, there's just no room for that kind of complexity when using the same file format. The solution is to generate the track data dynamically using code rather than hard-coded data tables, and that's the process that we're going to look at in this article.
Note that the following requires an understanding of how the tracks in Revs get built from sections, segments and segment vectors. For an explanation of these concepts, see the deep dive on building a 3D track from sections and segments. Understanding this approach is pretty key to understanding the way the extra tracks work, so it's worth having a quick look at the above before tackling the rest.
Also note that all the extra track files contain the same code and use the same approach; the only thing that differs is the data. Links in the following will take you to the source code for Oulton Park, but you could equally pick any of the five extra tracks.
The problem
-----------
So just how bad is this space problem, and why can't we store a track like Oulton Park in the standard track data file format? Let's take a look at the figures.
As noted above, curved track sections in Revs are stored as sequences of segment vectors, where each vector moves us from one segment to the next (i.e. from one orange dot to the next in the above images). There's one set of vectors for the inner verge, and another for the outer verge. The inner verge's segment vectors each have three coordinates (x, y and z) and define the 3D vector from one segment to the next, working along the inner edge of the track. The outer verge's segment vectors define the vector from the inside of the segment to the outside of the segment, and as each track segment is level from left to right, there is no change in height as we move from one side of the segment to the other. This means that the outer verge's segment vectors only need two coordinates (x and z), as we know the outer vector's y-coordinate is always zero.
The segments are small enough that each of the segment vector's coordinates fits into one byte, and the track data file has room for 256 segment vectors. As there are five coordinates per vector, that's a total of 5 * 256 bytes, or 1,280 bytes to store all 256 segment vectors. Given that each track data file is 1,849 bytes in total, that means 69% of the Silverstone track data file is taken up by segment vector data.
That works for Silverstone, but what about Oulton Park?
Out of the 27 track sections in the Oulton Park track, only eight of them are straight, and half of those include changes in track elevation, so using the Silverstone model, they would still have to be encoded as curves. That leaves us with 23 curved track sections, and there's no way you could fit all those curves into just 256 segment vectors; indeed, Oulton Park consists of 819 segments, with only 191 of those appearing on completely straight sections, so that leaves 628 curved segments, each of which needs an inner and outer segment vector. 628 is more than double the 256-vector capacity of the original track data file format, so there is nowhere near enough space.
The other extra tracks have the same problem, but Revs 4 Tracks still came out for Christmas 1985 as planned, with the new tracks crammed into the same track data file system as Silverstone. There is no updated Revs binary provided with the expansion pack - you need the original game to load these tracks, and the expansion only contains the four track data files, along with a BASIC program to let you choose which one to load.
So how do the extra tracks implement all these extra curved sections, and without needing a new version of the main game? Let's take a look.
Dynamic generation of segment vectors
-------------------------------------
Geoff Crammond's solution to the above problem is characteristically elegant. Instead of devoting 69% of the track data file to segment vectors, the extra track files contain code in place of the data. This code contains a number of modifications to the main game code, most of which are nothing to do with segment vectors; see the deep dive on secrets of the extra tracks for details of how the code modifications in the extra track files work, and see the deep dive on code hooks in the extra tracks for details of all the modifications.
Part of the code in the extra track files is responsible for generating the track's segment vectors on-the-fly, as they are needed. This removes the need for the five large data tables, which are instead replaced by smaller versions that wrap around to fit into just 40 bytes each, rather than 256 bytes. This complexity is hidden from the main game code, which still fetches segment vectors from the segment vector tables as usual, but behind the scenes, the routines in the extra track file populate the track data tables before they are read.
There are four hook routines that are injected into the main game code to generate segment vectors dynamically. These routines are identical across all the extra tracks, and between them they update the main game code so that it fetches track segment vectors dynamically, rather than blindly reading them from a data table. They are as follows:
- HookSectionFrom gets injected into the GetSectionCoords routine. It gets called whenever the main game code wants to fetch section coordinates from the track data file. It initialises all the variables associated with the dynamic generation of segment vectors and calculates the current track segment vector.
- HookFirstSegment gets injected into the GetFirstSegment routine. It gets called whenever the main game code wants to fetch the first segment in a new section, and calculates the first segment vector within the new section.
- HookDataPointers gets injected into part 1 of the GetTrackSegment routine. It updates the various pointer variables used for dynamic track generation.
- HookSegmentVector gets injected into part 3 of the GetTrackSegment routine. It generates the track segment vector, ready for it to be read.
See the deep dive on code hooks in the extra tracks for the exact details of how these modifications are applied.
Underlying these routines are quite a few variables and subroutines, which generate the track data required by the main game. Let's take a look at how segment vectors are generated on demand by the hook routines above.
Encoding curves
---------------
In the Silverstone track, each segment vector is stored as exactly that - a vector. For the inner segment vectors, this is the vector that takes us from the current segment to the next segment, so we can construct a track section by taking the starting coordinates for the section, and adding the relevant inner segment vectors to work our way along the track verge, one segment at a time. Given the segment's inner coordinates, we can calculate the segment's outer coordinates by simply adding the outer segment vector to take us from the inner verge to the outer verge.
As noted above, Silverstone stores these segment vectors as coordinates, with three coordinates for the inner segment vector and another two coordinates for the outer segment vector. In a sense, the segment vectors encode a set of instructions for building the track that go something like this:
- Go to the section's start coordinates
- Step along the track by the first inner segment vector for this section
- Step along the track by the second inner segment vector for this section
... - Step along the track by the last inner segment vector for this section
- Go to the next section's start coordinates
- Step along the track by the first inner segment vector for this new section
...
Each step along the track creates one track segment, represented by a dot in the images above. For curved sections, there is a different segment vector for each step along the section, while for straight sections, we use the same segment vector for each step along the straight line. The segment vector tables describe the shape of the track by effectively storing the shape of each individual segment.
In the extra tracks, the shape of the track is encoded differently. The track is not only broken down into sections, but it's also broken down into sub-sections, and the sub-sections are then broken down into segments (so there is an extra layer of abstraction when compared to Silverstone, though sections and segments are still the same, it's just that there's an additional layer between them). For the extra tracks, the track-building instructions look more like this:
- Go to the section's start coordinates
- Calculate the direction of the track at the start of the section
- Fetch the size and curve characteristics of the first sub-section's curve
- Step along the track for the length of the first sub-section, starting in the track direction, and updating the direction at each step by the curve characteristics
- Fetch the size and curve characteristics of the second sub-section's curve
- Step along the track for the length of the second sub-section, updating the direction at each step by the curve characteristics
... - Fetch the size and curve characteristics of the last sub-section's curve
- Step along the track for the length of the last sub-section, updating the direction at each step by the curve characteristics
- Go to the next section's start coordinates
- Calculate the direction of the track at the start of this new section
...
We'll talk more about sub-sections below, but they essentially break the track down into smaller curves that each have a constant rate of change. The "curve characteristics" mentioned above are the rate of change of the track's direction, expressed in terms of a yaw angle delta and a slope delta (i.e. a change in compass heading and a change in slope).
We'll explain all these terms in a minute, but the important thing is that the second approach codifies the track shape in far less data. Instead of needing to store three coordinates for every segment, we only need to store the curve characteristics once for each sub-section, plus the size of the sub-section in terms of segments, and we can calculate the inner segment vectors from that starting point. Larger sub-sections take up no more space than smaller sub-sections; they only differ in the segment count, not the amount of data required.
The outer segment vectors are similarly simplified in the extra tracks. In Silverstone, each outer segment vector requires two coordinates, but in the extra tracks, the outer segment vectors are calculated from the inner segment vectors; in essence, the outer segment vector is set to the normal vector of the inner segment vector, as this gives us the vector from the inside of the track to the outside (more on which below). Importantly for us, the outer segment vectors don't need any storage in this approach.
The Silverstone data format is more flexible in that you can encode absolutely any kind of track shape, while the extra tracks have to break the track down into sub-sections, each of which has a constant rate of change in terms of compass heading and slope. In practice, this isn't a problem, as that's how racing tracks tend to be built - from sequences of regular curves.
Let's look at how this new algorithm is implemented in the extra tracks.
Curve characteristics
---------------------
In the new system, each track section has two important bits of associated data:
- The first is the section's yaw angle, which defines the direction of the track at the start of the section. This can be thought of as a compass heading for the beginning of the section, and it's expressed in terms of the following set of angles (see the deep dive on pitch and yaw angles for more details on angles in Revs):
0 224 | 32 \ | / \ | / ^ \|/ | 192 -----+----- 64 + Overhead view, looking north /|\ / | \ / | \ 160 | 96 128So if a track section has a yaw angle of 96, then the track at that point is heading south-east. These yaw angles are stored as 16-bit values in the track's (trackYawAngleHi trackYawAngleLo) tables, with the high byte representing an angle from 0 to 255 as in the above diagram, and the low byte representing a fractional part of the angle (so 0 to 65536 represents a yaw angle of 0.0 to 256.0, covering the whole compass circle above). - The second is the vertical slope, i.e. the gradient of the track at the start of the section. This is stored as the y-coordinate change over the course of the section's first segment vector - i.e. the amount we would add to the section start y-coordinate to get the y-coordinate of the first segment.
So given a section number, we can look up the compass direction and slope of the track at the start of that section. This gives us the direction in all three axes that the track is heading in at the start of the section, in terms of yaw angle and slope.
On top of this, each sub-section has a number of associated data that we use to generate the track. They are:
- The yaw delta, which is a 16-bit value in (trackYawDeltaHi trackYawDeltaLo) that describes the change in yaw angle for each step (i.e. each segment) along the sub-section
- The slope delta, which is an 8-bit value in trackSlopeDelta that describes the change in slope for each step (i.e. each segment) along the sub-section
- The sub-section size in trackSubSize, which defines the number of segments in each sub-section
To generate the segment vectors for a sub-section, we start by initialising all the variables we need. This is done in the HookSectionFrom routine, which fetches the yaw angle and slope for the relevant section and stores them in the (yawAngleHi yawAngleLo) and segmentSlope variables.
We then step along the track, one segment at a time, and for each segment, we add the yaw delta to the yaw angle, and we add the slope delta to the gradient. This is done in the SetSegmentVector routine, where the yaw angles are added using 16-bit arithmetic, with the low byte representing the fractional amount. This means that within a sub-section, the track turns by the yaw delta for each segment, and the gradient increases or decreases by the slope delta for each segment. The yaw delta and gradient therefore describe the shape of each sub-section, and each sub-section is a regular shape, in that both the yaw angle and the slope change at the same rate for every segment within that sub-section.
In this way, as we step along the segments, we can update the direction of the track in three dimensions, just by adding on the two deltas at each step. What we need, though, is the segment vector - i.e. the 3D vector from each segment to the next - as that's what the main game code expects. The conversion of the current direction (i.e. yaw angle and slope) into a 3D segment vector is performed by the CalcSegmentVector routine, which takes the current yaw angle in (yawAngleHi yawAngleLo) and the current slope in segmentSlope, and produces a 3D vector equivalent that's parallel to the track direction and is the length of a segment. This is then stored in the (xTrackSegmentI yTrackSegmentI zTrackSegmentI) tables in the track data file, ready for the main game code to read.
At the heart of this conversion process are the curve tables at xTrackCurve and zTrackCurve. Between them, these two tables contain the tangent vector (i.e. the curve direction) at 64 points on a one-eighth circle covering 0 to 45 degrees. The CalcSegmentVector routine reduces the current yaw angle of the track down to a quarter circle, looks up the tangent vector at that point on the circle from the xTrackCurve and zTrackCurve tables, and then uses this to calculate the tangent vector for the full yaw angle by flipping signs and reflecting the result (in much the same way as the trigonometric functions described in the deep dive on trigonometry).
This tangent vector gives us our inner segment vector, as it's a vector with a one-segment length and an angle that matches the track's yaw angle at this point - in other words, it's the vector from this segment to the next, in the direction of the track. This gives us the x- and z-coordinates of the segment vector, and we can use the value of segmentSlope for the y-coordinate to complete the picture. Also, it's worth noting that the yaw angle calculations are done in 16-bit arithmetic, but only the top byte is used for looking up the curve, so although there are 64 curve vectors in a quarter-circle, the underlying yaw angle calculations are much more accurate than this.
So that's the inner segment vector generated, but what about the outer segment vector? Well, the vector we fetched from xTrackCurve and zTrackCurve has a fixed length, so we can use it to calculate the vector from one side of the track to the other. Given a 2D vector [V W], the vector [-W V] is the vector's normal, i.e. the same vector, but perpendicular to the original. So if we take the inner segment vector in [V W], then its normal vector is a vector that's perpendicular to the original, so instead of being a vector pointing along the inner edge, it's a vector pointing at 90 degrees across the track, which is the vector that we want to calculate.
Multiplying the normal vector by the track width sets the correct size for the vector across the track, and this calculation gives us our outer track segment vector. Each track has its track width defined in the configuration variable trackWidth, so if we wanted, we could make the track wider by changing this value (as long as we also moved the outer section coordinates by the same amount).
The final step in the CalcSegmentVector routine is to store the resulting inner segment vector in the xTrackSegmentI, yTrackSegmentI and zTrackSegmentI tables, and the outer segment vector in the xTrackSegmentO and zTrackSegmentO tables. We do this at the offset given in thisVectorNumber, which always points to the current segment vector number. In this way, we can write the segment vector values to memory, knowing that when the main game code fetches the vector given by thisVectorNumber, it will fetch the data that we just stored.
That, in a nutshell, is how the Revs extra tracks generate segment vectors on-the-fly. Next, let's take a closer look at how sections and sub-sections work together.
Sub-sections
------------
As mentioned above, the extra tracks are not only broken down into sections, but they're also broken down into sub-sections. For example, in Oulton Park, there are 27 track sections (0 to 26) that between them contain a total of 58 sub-sections (0 to 57). These two concepts work together, so the track is made up of section 0, then section 1, and so on up to section 27, and the track is equivalently made up of sub-section 0, then sub-section 1, and so on up to sub-section 57.
The trackSubConfig and trackSubSize tables contain the details of the sub-section structure of the track. The first table, trackSubConfig, contains one entry for each section, as follows:
- Bits 2 to 7 contain the number of the first sub-section in this section
- Bit 1 isn't used by this part of the code (it's horizon-related)
- Bit 0 determines the type of generator to use; if this is set, then the segment vectors for this section are generated for a straight track rather than using the curve tables (see the part about straight sections below for more details)
So looking at the trackSubConfig table for Oulton Park, we can see that section 0 starts with sub-section 0, section 1 starts with sub-section 4, section 2 starts with sub-section 7, and so on. From this, we can work out that:
- Section 0 contains sub-sections 0, 1, 2 and 3
- Section 1 contains sub-sections 4, 5 and 6
The second table, trackSubSize, contains the number of segments in each sub-section, so looking at the trackSubSize table for Oulton Park, we can work out that:
- Sub-section 0 contains 2 segments
- Sub-section 1 contains 18 segments
- Sub-section 2 contains 3 segments
- Sub-section 3 contains 22 segments
- Sub-section 4 contains 8 segments
- Sub-section 5 contains 6 segments
- Sub-section 6 contains 5 segments
The HookSectionFrom routine uses this information to initialise the subSection and subSectionSegment variables when we need to start generating segment vectors for a new section. The subSection variable gets set to the number of the first sub-section in the current section (from trackSubConfig), while subSectionSegment keeps track of the number of the segment within the current sub-section, so it gets initialised to 0, as we're at the start of a new sub-section.
We use these variables to keep track of the sub-section and segment numbers as we build the track, and the UpdateDataPointers routine updates their values when we need to move on to the next segment (by either moving on to the next segment, or back to the previous segment).
As we move through the segments, we also update the value of thisVectorNumber, which points to the offset of the section's first segment vector within the segment vector tables at xTrackSegmentI, yTrackSegmentI, zTrackSegmentI, xTrackSegmentO and zTrackSegmentO. This variable is used by the main game code to access the current segment vector, but it works slightly differently in the new system.
In Silverstone, thisVectorNumber is a number in the range 0 to 255, as the segment vector tables are all 256 bytes long. In the extra tracks, we have ditched these huge tables and replaced them with dynamic generation of segment vectors, so we can reduce the tables to 40 bytes each. We choose this size to match the size of the track segment buffer, so we can store enough generated segment vectors to cater for all the segments in the buffer - see the deep dive on data structures for the track calculations for details on the track segment buffer.
To make sure that thisVectorNumber points to the correct position in the 40-byte segment vector tables for each section, we can set it to the segment number at the start of the section, modulo 40. This allows us to point thisVectorNumber into the smaller segment vector tables, by keeping the index within the range 0 to 39, while still ensuring that segments in the table are ordered in the same way as they are on the track. These modulo values are stored in trackSectionFrom in part 2 of the track section data, and are fetched to use as the value of thisVectorNumber for each section in exactly the same way as for the Silverstone track.
That's how sub-sections work, so let's finish off with a look at straight sections.
Straight sections
-----------------
We have talked a lot about generating curves, but straight sections are just as vital, so how do these work? Not surprisingly, they work in the same way as straight sections in the original Silverstone track, but the single segment vector that is required for straight sections is generated rather than read from a hard-coded table.
There is one potential source of confusion that it's good to be aware of. In the original track data file, bit 6 of the track section flags in trackSectionFlag has no effect, and is ignored. In the extra tracks, this bit defines whether to generate this section as a curve, i.e. using yaw angles and slopes, or whether it's a straight section. When bit 6 is set, the section is generated as a curve, but when it's clear it's generated as a straight. Interestingly, this same bit of data is duplicated in bit 0 of trackSubConfig, which always matches bit 6 of trackSectionFlag, so there are two places in which the generator type is defined.
When bit 6 of trackSectionFlag and bit 0 of trackSubConfig are clear, then the HookDataPointers routine skips updating the sub-section and segment pointers, the HookSegmentVector routine doesn't do anything at all, and SetSegmentVector doesn't add the deltas to the yaw angle and slope, so we don't change the segment vector for each new segment. This leaves the last segment vector from the end of the previous section in the table, so this is used as the segment vector for the entire straight section. Keeping the same segment vector throughout the whole section gives us a straight section that doesn't veer left or right, as well as keeping the same gradient, which is exactly how straight sections work in the original track data file.
Note, however, that a section can be generated as a curve with bit 6 of trackSectionFlag and bit 0 of trackSubConfig set, but it can also have bit 0 of trackSectionFlag clear, to denote a straight section. This works because the hook routines take care of updating the pointers, so they control whether the section is a curve or a straight, but bit 0 is still used throughout the main game code to denote a "straight" section when it comes to things like computer assisted steering, the other drivers' behaviour, corner markers and so on. In this way it's possible in the extra tracks to have straight sections that aren't perfectly straight, but which otherwise behave correctly.
Overall, the track generation system is a neat solution to the challenge of squeezing sophisticated curved tracks into tiny data files. In the extra tracks, it's not only the car that's powered by an engine - so is the track data file. It's very elegant stuff.